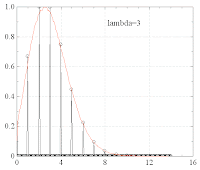
The following plot compares the discrete PDF (black) with the continuous one (orange) for lambda=3:
The same for lambda=33:
Theoretically, the kurtosis of the discrete Poisson distribution is 1/lambda. The following plot compares the numerical kurtosis=f(lambda) in the discrete (orange) and in the continuous version (green) with the analytical expectation (black):
The continuous Poisson distribution is obviously related to the gamma distribution with a=k+1. However, in the gamma distribution with shape parameter a and rate parameter b,
![G_{a,b}(x)=\left[b^a /\Gamma(a)\right] \;x^{a-1} e^{-bx}](https://lh3.googleusercontent.com/blogger_img_proxy/AEn0k_sd6iJ7AdsMD4Lt5weWUmZjspiK0ZP6RFM0RxmfLhPCgaY54zgU0zd96CjQt7b8KuYCLUL0FUeZ6hyRTEQyZ8VWy13MUyucD3Y1R8N68eo9v_56ooGP2XgwMA9apOUJsuQ9_uhWllFYjWPyovMYAeFd1BWnh6_ImWpugSCV70ItXIz4WqKr783CFZ9mpaN9r4Czkf7E4sB9jxcN6swrWcUokP0hjQoESWbdjOYO=s0-d)
it is x=lambda which is considered as the random variable.
Hi, what about normalization? I could not find any analytic result that helped me integrate \lambda^k / \Gamma(k+1) .
ReplyDeleteGreat! Thanks
ReplyDeleteHi, do you know how to sample from the continuous Poisson distribution, i.e. k is replaced by a continuous variable x?
ReplyDeleteIt seems MATLAB or R can only generate random numbers from discrete Poisson distribution. Where is a generator for the continuous version?
Hi, do you know how to sample from the continuous Poisson distribution, i.e. k is replaced by a continuous variable x?
ReplyDeleteIt seems MATLAB or R can only generate random numbers from discrete Poisson distribution. Where is a generator for the continuous version?
There is no continuous Poisson distribution. What has been discussed is a potential continuous extension of the Poisson. So it is not surprising that MATLAB or R will have only the discrete distribution. However, you may write your own little code to draw samples from a uniform distribution, then apply the inverse function to get random numbers from any distribution you please.
Delete