[AD 16] Effect of microstep rate on MSD and PSD

If the Poisson statistics is combined with the s*d process, the VAC depends on the system parameters as follows:


While w_1 merely affects the scale of correlated bead fluctuations, the number of microsteps lambda per discretization intervall enters non-linearly into the formula.

The following plot shows the effect of lambda on the MSD:



And, even more pronounced, on the PSD:



The parameters were as follows:

sigN2=0.5e-4; // variance of white noise [um^2]
beta=1.5; // PL exponent of MSD [1]
lambda=2.0; // aver. nr. of microsteps per dT [1]
w1=5.0e-3; // width of single microstep [um]

It is inctructive to compare this with the effect of changing w1 at fixed lambda. The MSD:



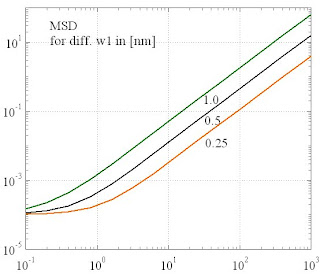
The PSD:


Obviously, the effects are rather similar. This comes in handy, when lambda is adjusted to fit the experimental kurtosis. Then the simultaneous changes in the MSD/PSD can be compensated via w_1.